An Analysis of Air Pollutant Transport
1. Introduction
We model the transport of air pollutants using a convection-diffusion equation to examine the effectiveness of long distance pollutant transport under strong winds. We use a mixed finite element scheme that is positivity preserving (even in the presence of sink terms!).
The example below shows the transport under wind speeds of 4-5 [km/h] with a constant pollutant source (such as industrial smoke or agricultural crop residue burning).
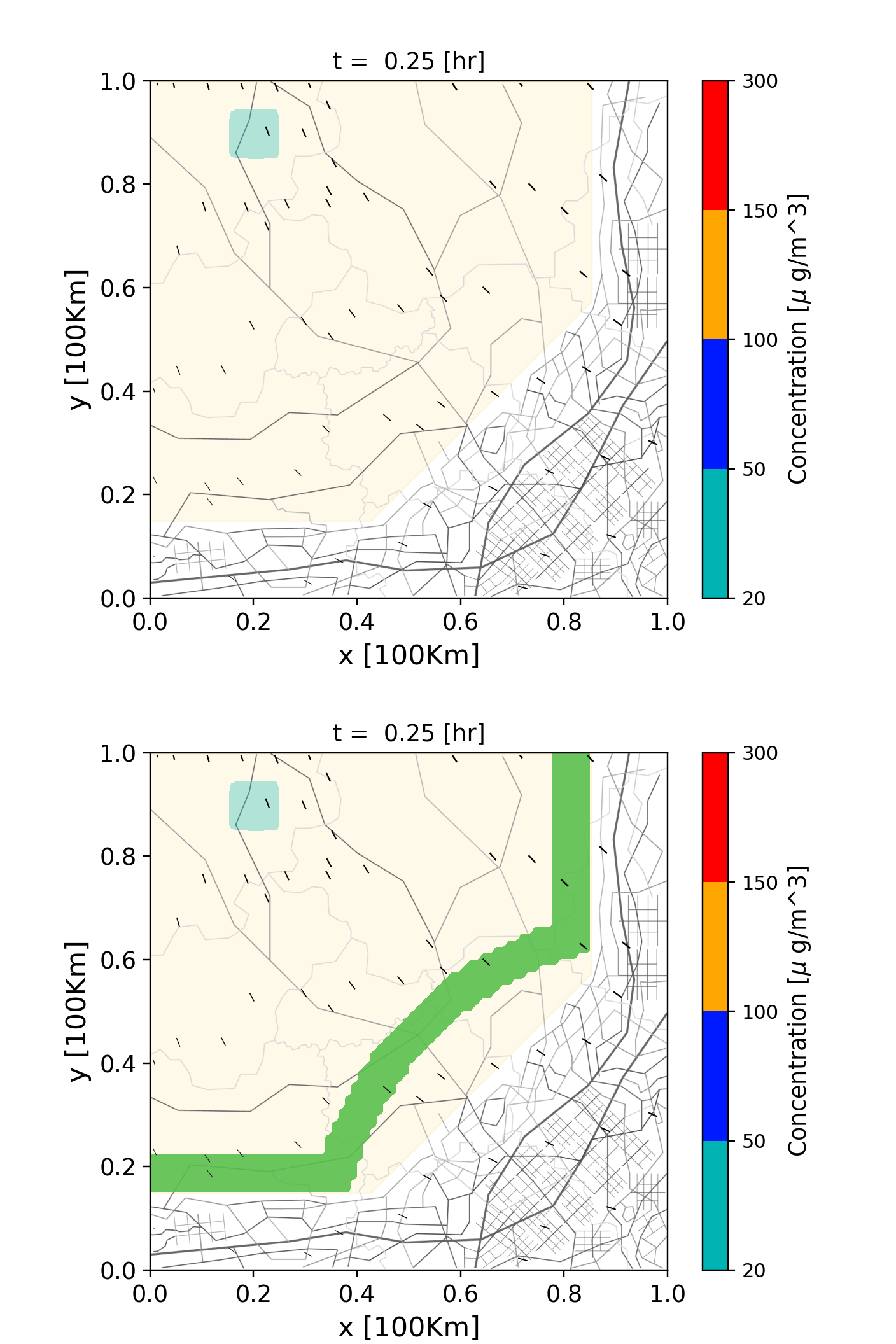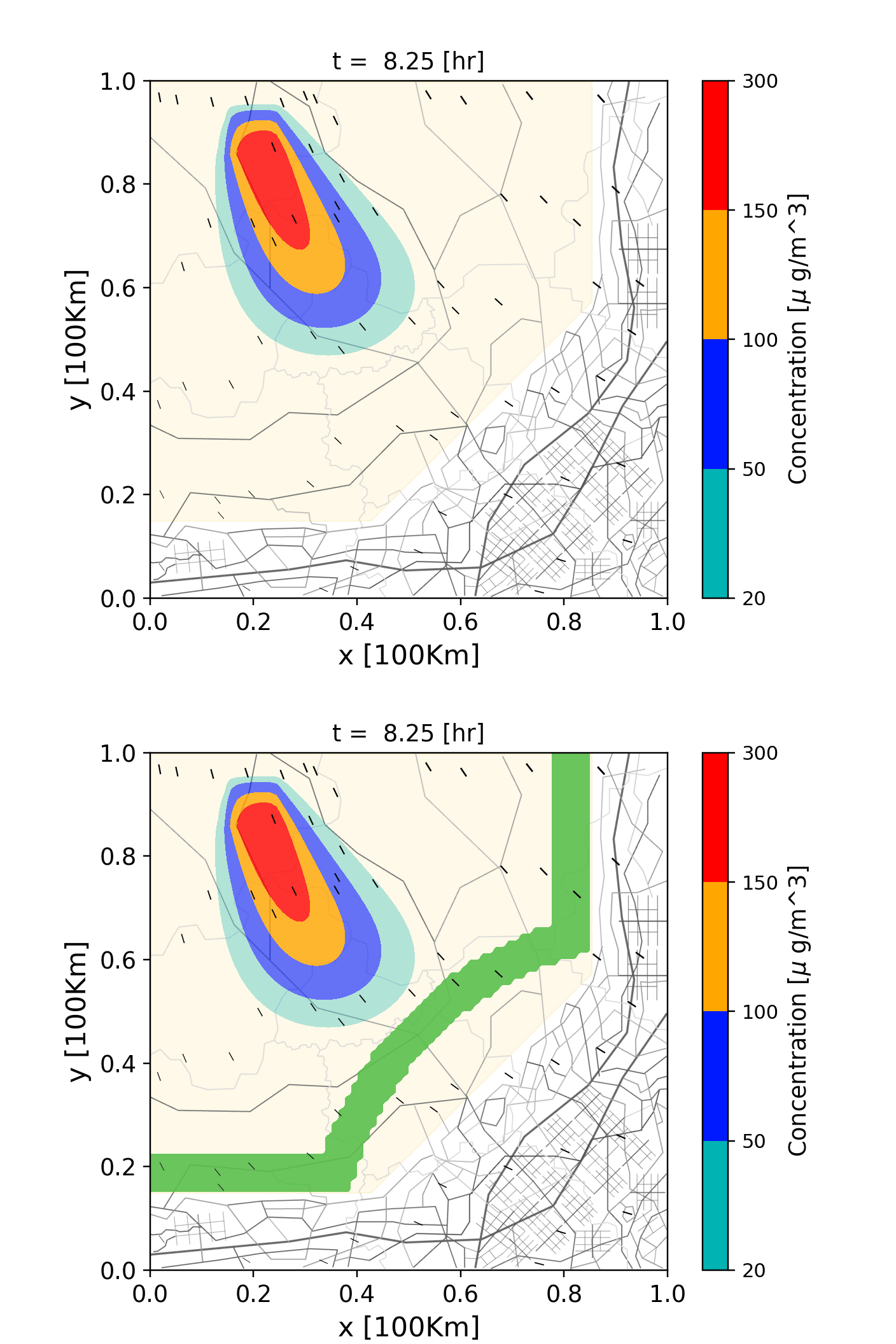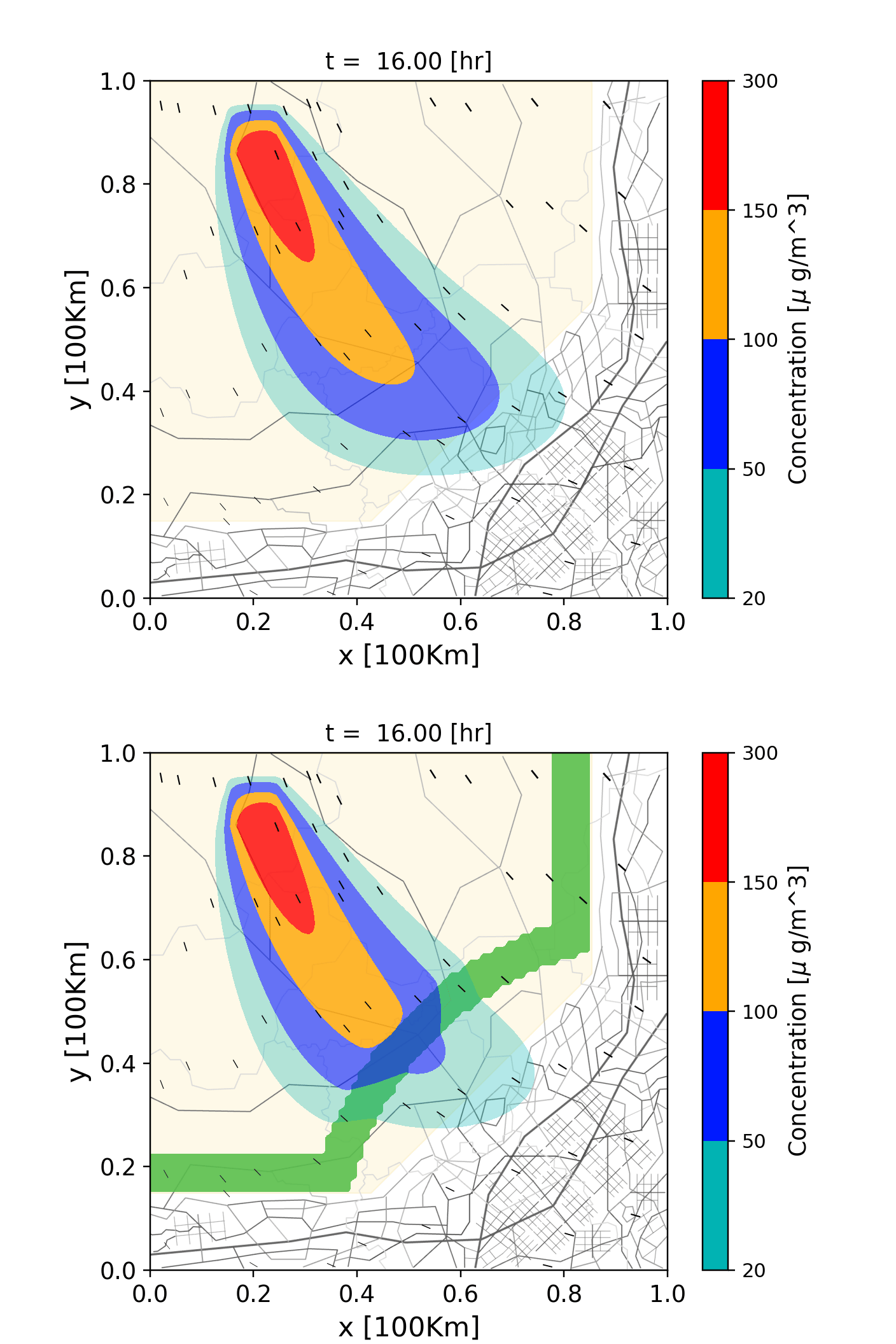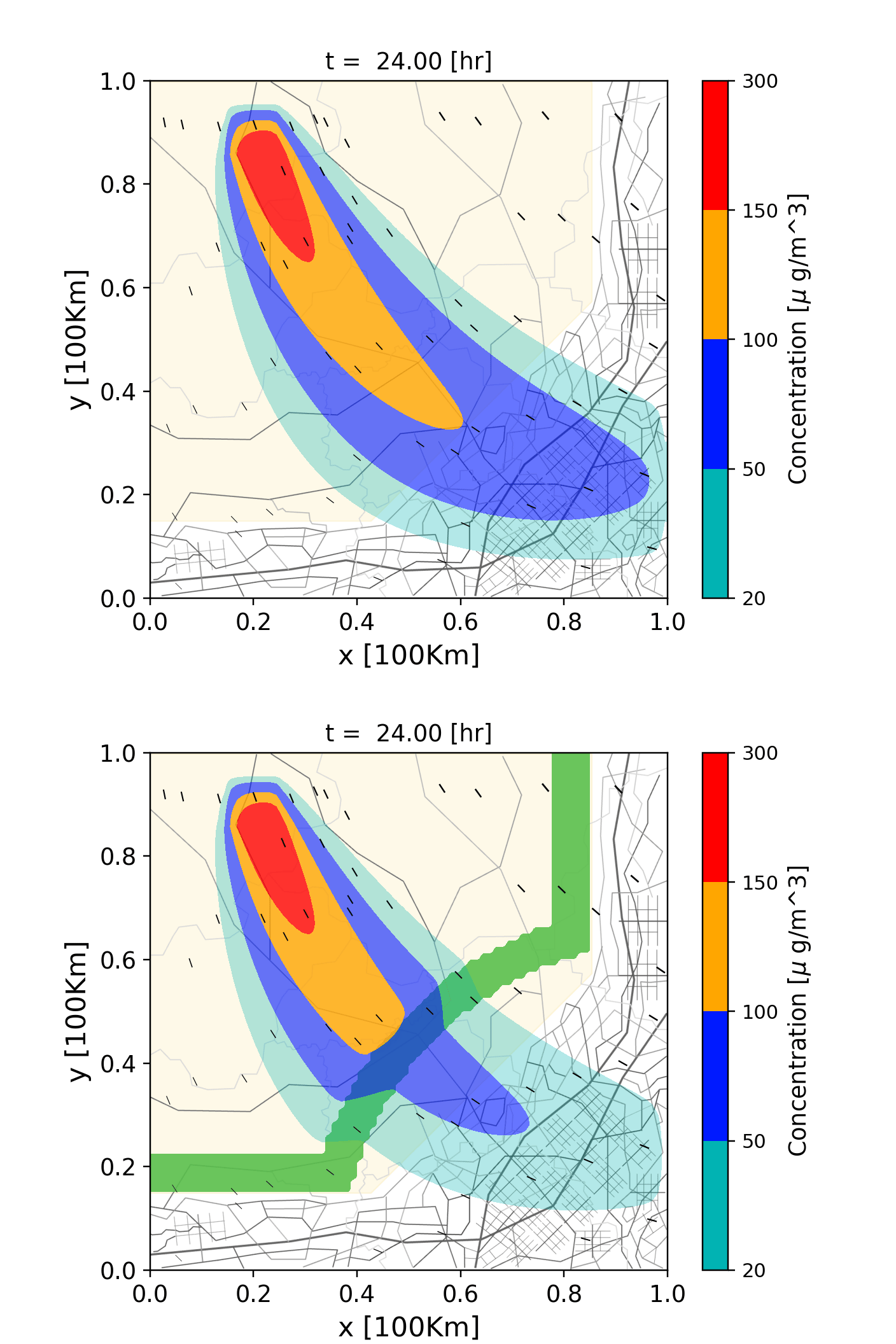
Figure 1. Simulation showing transport of air pollutants under strong winds.
