Profitability of Batteries Performing Arbitrage in Wholesale Markets with Cyclic Degradation
1. Battery Energy Storage Systems Model
Battery Energy Storage Systems (BESS) hold an important role in various avenues of power systems, from complementing renewable energy sources (such as Solar) to participating in electricity markets for arbitrage and ancillary services. The basic set of linearized equations for BESS are as follows1
\begin{equation} \label{eq:SOC} SOC_n = SOC_{n-1} + \tau\left(\eta P^c_n - \frac{1}{\eta}P^d_n\right) \end{equation}
where $SOC_n$ [MWh] is the state of charge at time step $n$, $P^c_n, P^d_n$ [MW] are the charge and discharge rates of the battery, respectively, $\eta$ [-] is the round trip efficiency, and $\tau$ [h] is the time step. The variables are further bounded $\forall n$
\begin{equation} \label{eq:BESS_constraints} P_{min} \leq P^c_n, \; P^d_n \leq P_{max}, \; 0 < SOC_{min} \leq SOC_n \leq SOC_{max} < E_B, \end{equation}
where $E_B$ [MWh] is the capacity of the battery.
1.1 Example: Arbitrage in wholesale electricity market
We consider a basic scenario where a given battery performs arbitrage in the wholesale electricity markets: that is, it charges up when the electricity prices are low and discharges when the prices are high, thereby marking a profit. If $\theta_n$ [Rs/MWh] is the wholesale market price at time step $n$, then we wish to find the optimial solution to
\begin{equation} \label{eq:objective} \text{minimize} \sum_{n} \left(P^c_n \theta_n - P^d_n \theta_n \right) \tau \end{equation}
given by eq. \ref{eq:SOC}-\ref{eq:BESS_constraints}.
We assume perfect foresight of the market prices, i.e., we assume prior knowledge of the wholesale market prices over the entire day at any given time.
We consider a $1$[MWh] battery with maximum charging/discharging rates $1$ [MW], and a round trip efficiency of $\eta = 0.9$. We take 15 [min] real time market prices (RTM) from IEX2 for the randomly chosen day of 15th February, 2025; see Fig. 1 below.
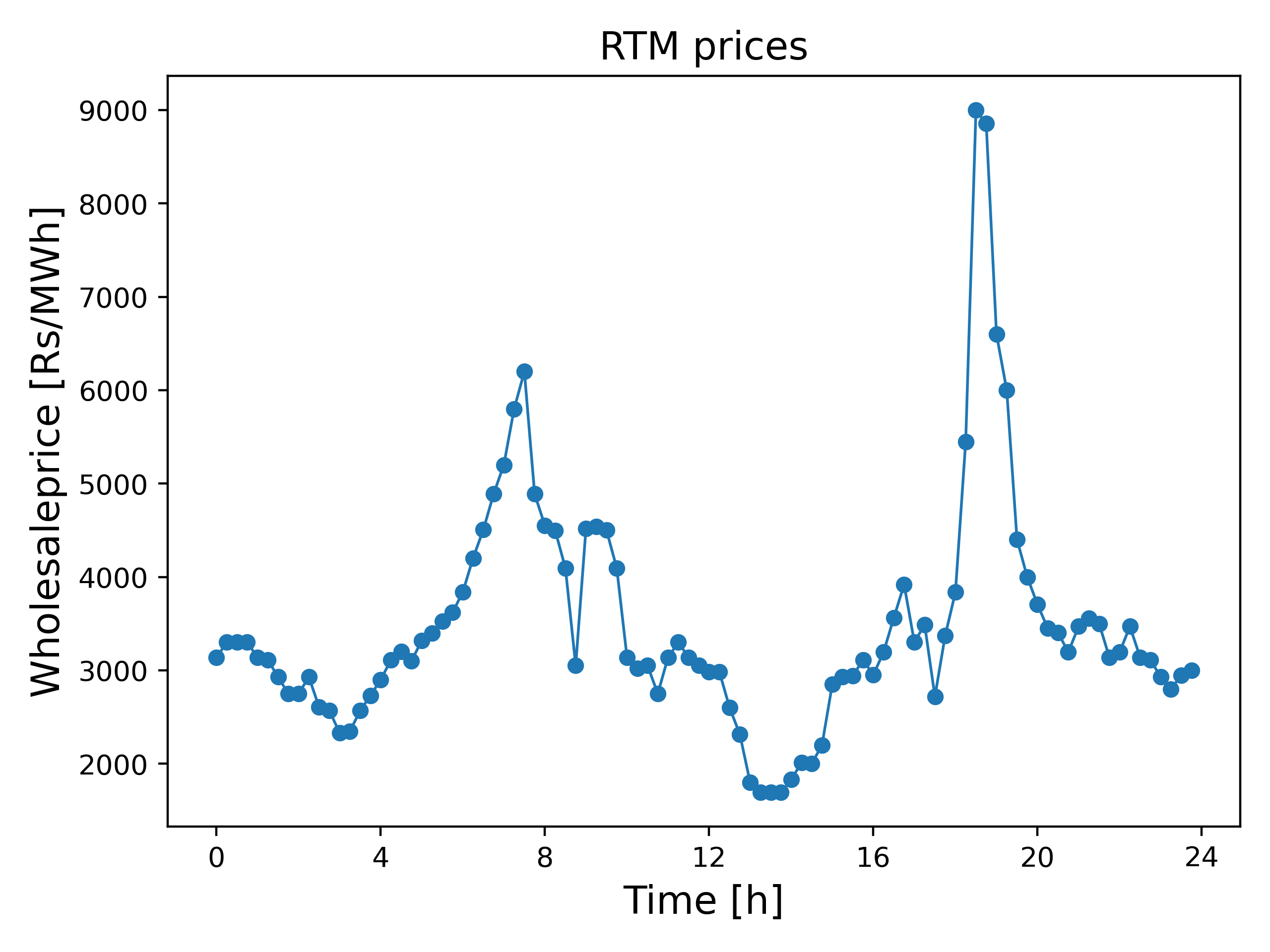
Results and discusion. The results are shown in Fig. 2 below.
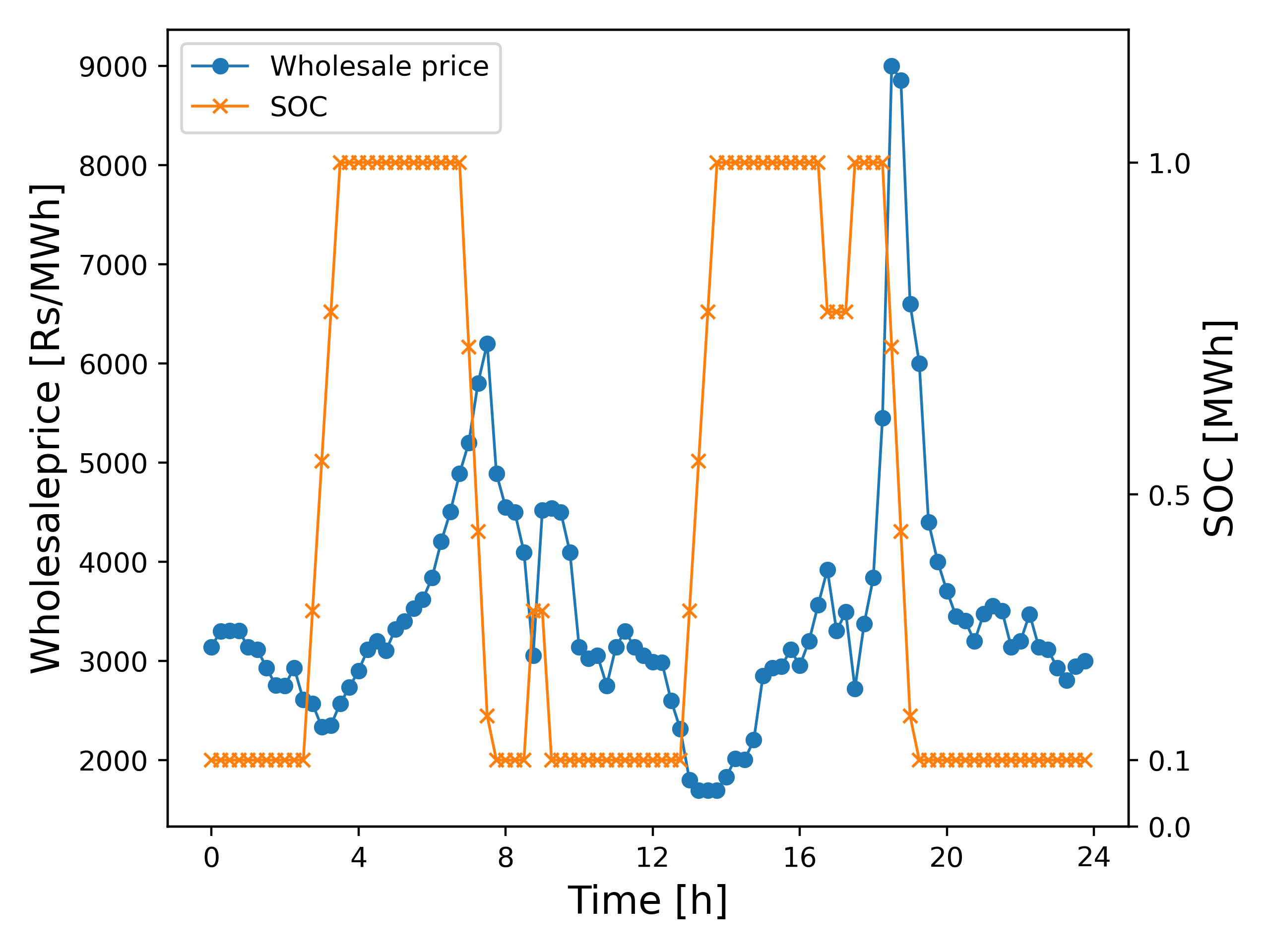
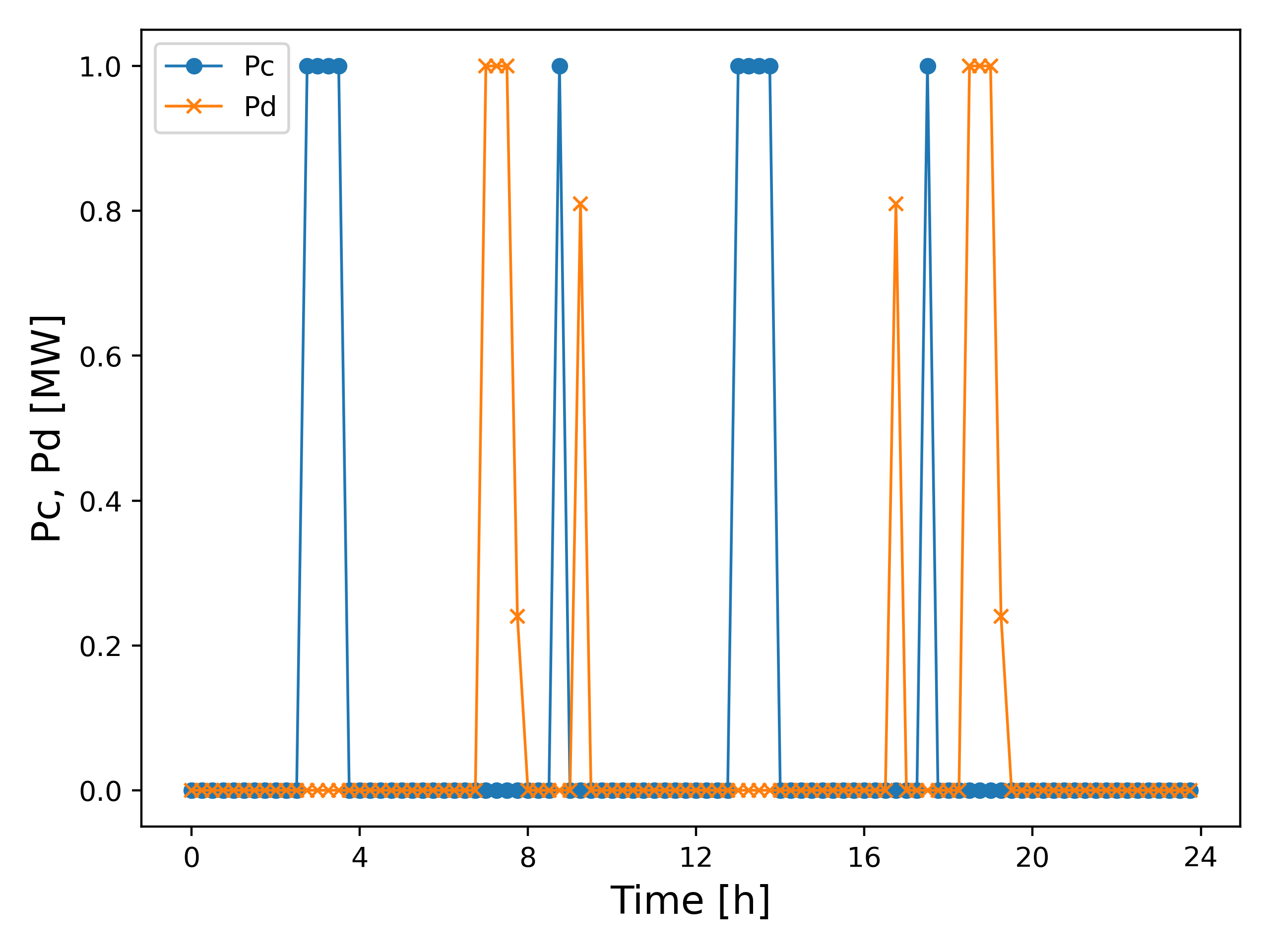
The battery follows two complete cycles following the peak electricity prices during the peak demand periods $t \approx 6$[h] and $t \approx 18$[h]. The battery first charges around $t \approx 4$[h] when the prices are at the lowest and discharges when the prices are high around $t \approx 8$[h]. Later in the day, the battery charges around $t \approx 13$[h] and discharges when the prices are highest around $t \approx 20$[h]. In this example, there are also two small charging/discharging periods following the local maximums of the prices around $t \approx 9$[h] and $t \approx 17$[h].
In this case the objective value comes out to be -28654.91 [Rs], indicating a net profit.
2. Accounting for Cyclic Degradation
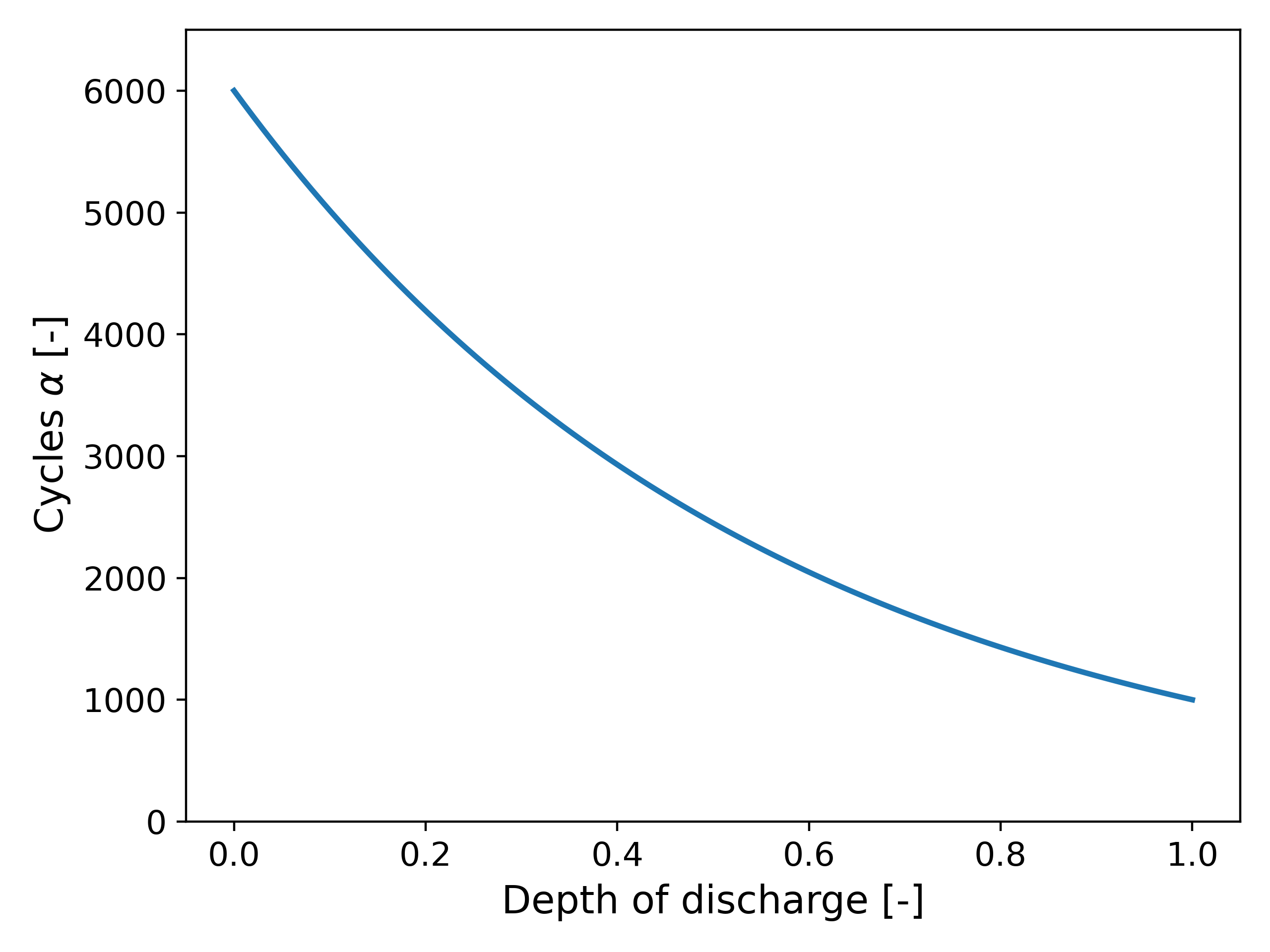
We now consider the degradation associated with battery cycling. Typically, the life of a battery (i.e., the number of cycles it is able to perform) depends on the depth of discharge (DOD) at which it is cycled, where the DOD is defined as the absolute difference between the state of charge in consecutive time steps divided by the capacity. We denote the cycles by $\alpha(DOD)$; see Fig. 3 for an illustration (adapted from3 using an exponential function).
If the cost of replacing the battery is $R$ [Rs], then the cost of one cycle is given by4
\begin{equation} \label{eq:cycle_cost} C^{cyc} = \frac{R}{\alpha\left(\delta \right)}. \end{equation}
Or, noting that the discharge rate associated with a DOD $\delta$ can be obtained from \ref{eq:SOC} as
\begin{equation} P^{d} = \frac{\eta E_B \delta}{\tau}, \end{equation}
we can rewrite \ref{eq:cycle_cost} as
\begin{equation} \label{eq:cycle_cost_pd} C^{cyc}\left(P^{d} \right) = \frac{R}{\alpha\left(\eta^{-1} {E_B}^{-1} \tau P^{d} \right)}. \end{equation}
Taking the cost of cycling into account, our objective function \ref{eq:objective} now becomes
\begin{equation} \label{eq:objective_cycles} \text{minimize} \sum_{n} \left(P^c_n \theta_n - P^d_n \theta_n \right) \tau + C^{cyc}\left(P^d_n \right). \end{equation}
The issue (slight!) with \ref{eq:objective_cycles} is that it introduces a nonlinearity in the objective function. To this end, we linearize the function $1/\alpha$ to provide an estimate of the solution to \ref{eq:objective_cycles}. Let $\beta_1, \beta_2 \approx 1/\alpha$ be two linear approximations such that $\beta_1 <= 1/\alpha <= \beta_2; see Fig. 4 for an illustration.
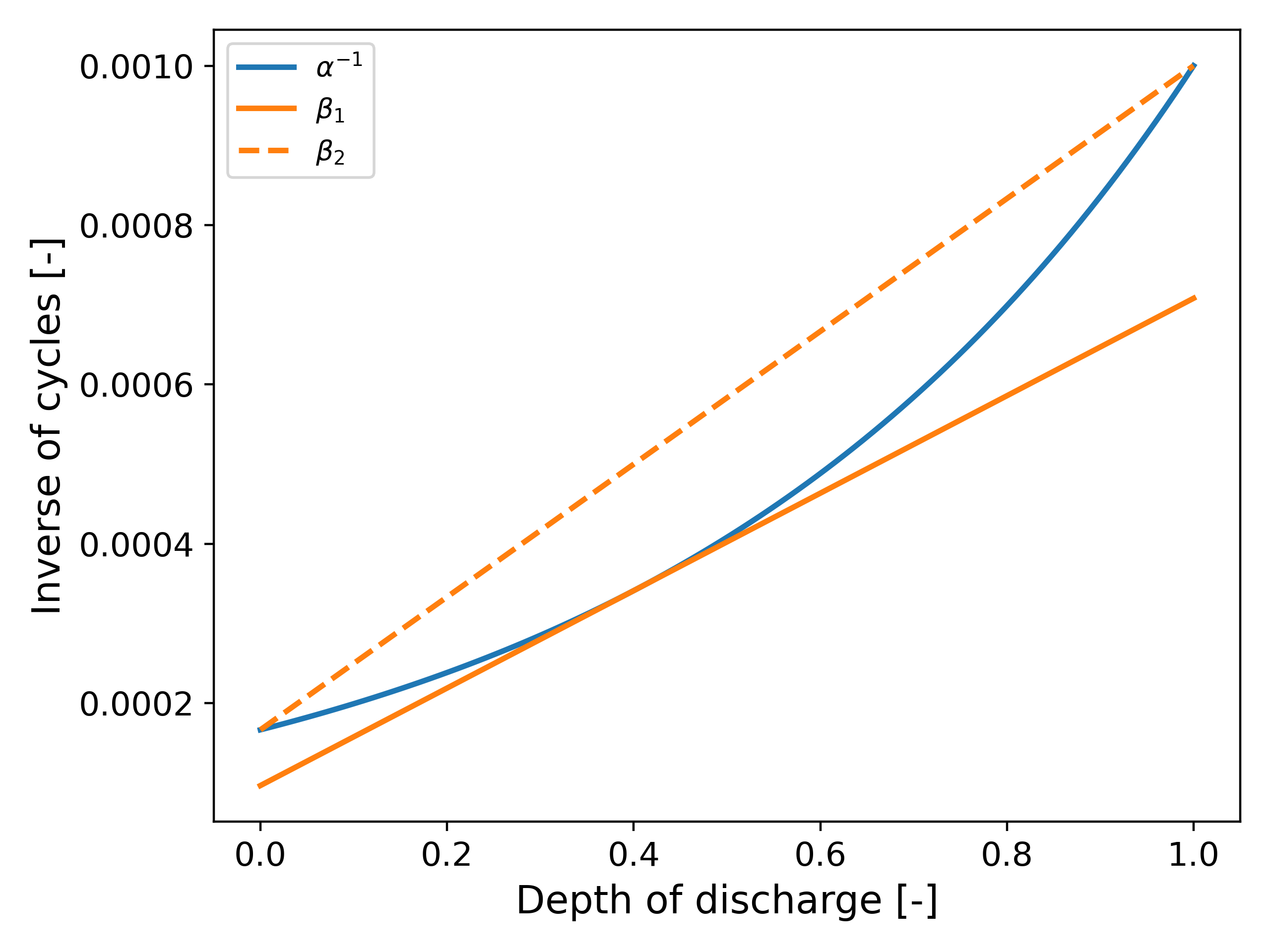
Note that the choice of $\beta_1$ and $\beta_2$ provide a bound for our objective function, and help us to under- and overestimate the net profits. We make this clear with the next example.
2.1 Example: Arbitrage with Cyclic Degradation
We now return to our example. We consider a replacement cost of $R = 2 \times 10^5$ [Rs] (see note below) and $E_B = 1$ [MWh]. We now consider the quarterly RTM prices taken from 1/8/2025 - 3/8/2025 from IEX2 (total of 72 hours). The cycle degradation curves are taken as in Fig. 3 and Fig. 4.
Results and discussion. The results are shown in Fig. 5 and Fig. 6.
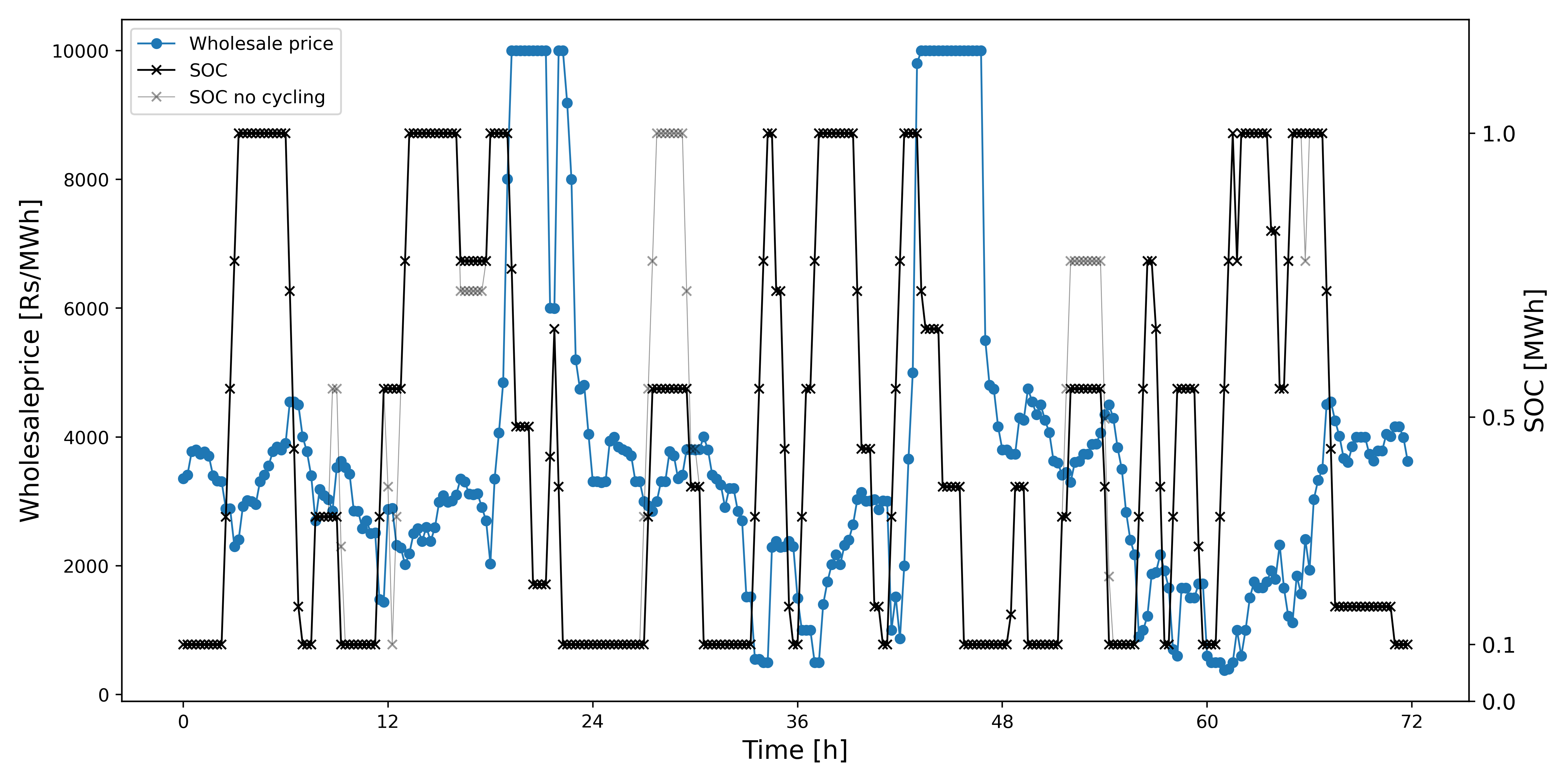
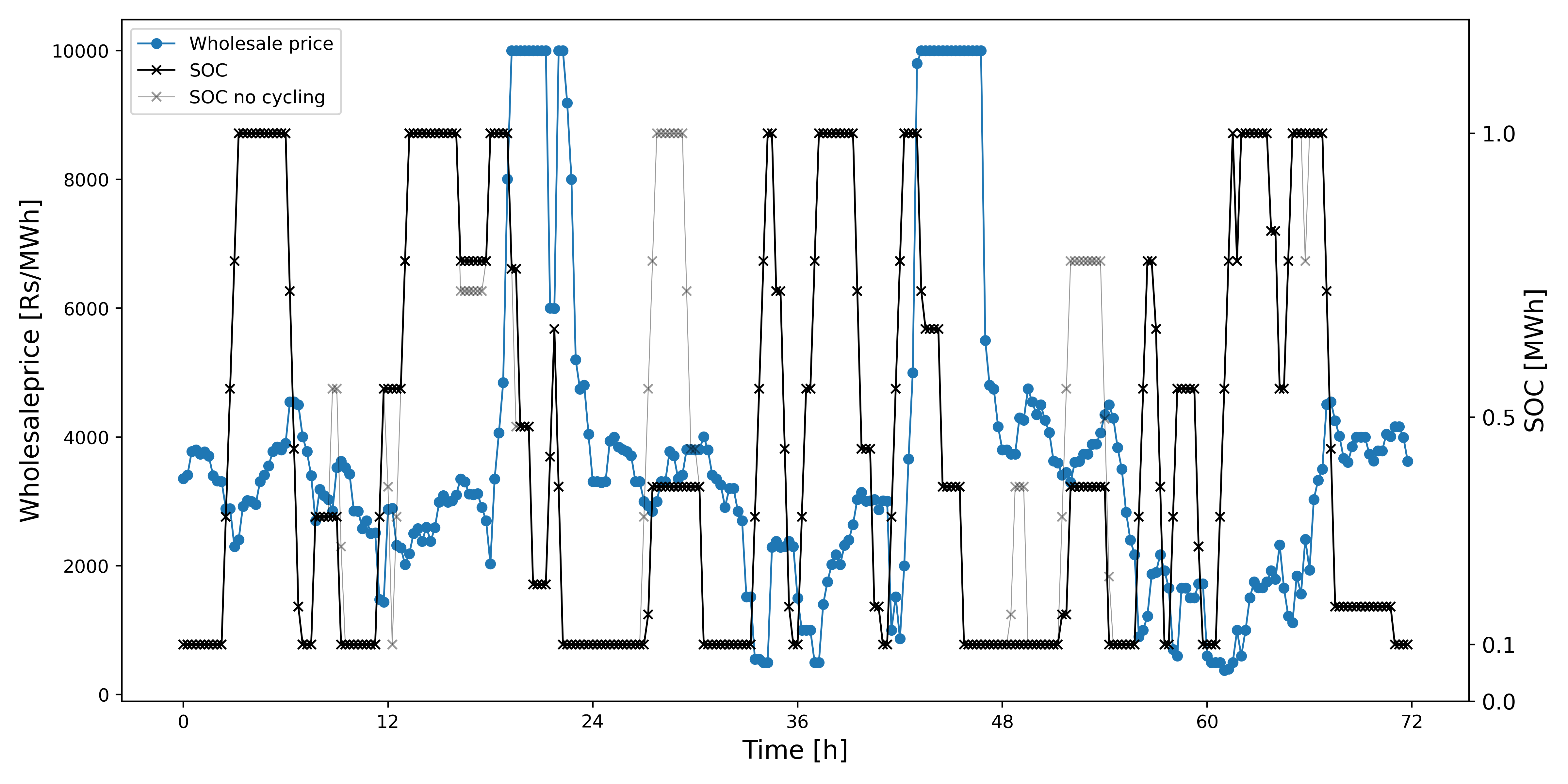
It can be observed that when cycle degradation cost is included, the battery cycles through smaller DOD values. For example, around $t \approx 30$[h], the battery only charges till an SOC $\approx 0.5$ when $\beta_1$ is used compared to $1$ earlier, and when $\beta_2$ is used it only charges till $\approx 0.25$ to minimize degradation costs. Moreover, around $t \approx 48$ [h], the battery does not charge at all when $\beta_2$ is used compared to earlier.
In case of $\beta_1$ and $\beta_2$, a net profit of $16398$ [Rs] and $11988$ [Rs] is made, respectively, and when no cyclic degradation is considered, the profit is $23162$ [Rs]. Our choice of linear approximations provides a profit interval of $[11988, 16398]$ in case a nonlinear solver were to be used to solve the system.
Note on choice of replacement cost R. We now justify the value of $R = 2 \times 10^5$ [Rs] used in the above example. The choice was made to clearly demonstrate the effect of cyclic degradation on arbitrage and cycling behaviour of the battery, and may vary from the actual cost of a $1$ [MWh] battery. If a higher cost of $R \approx O(10^7)$ is used, then the battery does not make a profit from the given wholesale prices and parameters. For known battery parameters, this examples also serves to provide a ballpark for $R$ for which the battery makes a profit.
Code
The code for the dispatch model has been written by the author using GAMS and Python. An equivalent code has also been developed in Pyomo5.
References
D. Pozo (2022), Linear battery models for power system analysis, Electric Power Systems Research, 212. ↩
Indian Energy Exchange (retrieved in 2025), https://www.iexindia.com/market-data/real-time-market/market-snapshot. ↩ ↩2
N. Padmanabhan, M. Ahmed, K. Bhattacharya (2020), Battery Energy Storage Systems in Energy and Reserve Markets, IEEE Transactions on Power Systems, Vol. 35, No. 1. ↩
Y. Shi et al. (2019), Optimal Battery Control Under Cycle Aging Mechanisms in Pay for Performance Settings, IEEE Transactions on Automatic Control, Vol. 64, No. 6. ↩
M. L. Bynum et al.,Pyomo - Optimization Modeling in Python, 2021, Springer, Third Edition Vol. 67. ↩
