Thermo-Hydro-Mechanical Analysis of Permafrost.
To study the land subsidence caused by thawing permafrost, one needs to analyze the coupling of the different mechanisms involved. Namely, these are deformation, flow, and energy. Analyzing these together, however, leads to numerically expensive complications and hence they must be studied individually and then coupled in a simpler fashion; see our brief overview article published in SIAM News Online here: Modeling Permafrost: Soil, Ice, and Some Really Hard Mathematics

Thermo-hydro-mechanical coupling
To couple flow [H], deformation[M], and energy [T], we need to consider thermo-hydro-mechanical models that take into account phase change [T] as well.

[HM]: Biot’s poroelasticity equations:
Flow [H] and deformation [M] can be modeled using Biot’s poroelasticity equations given below [1], [2]
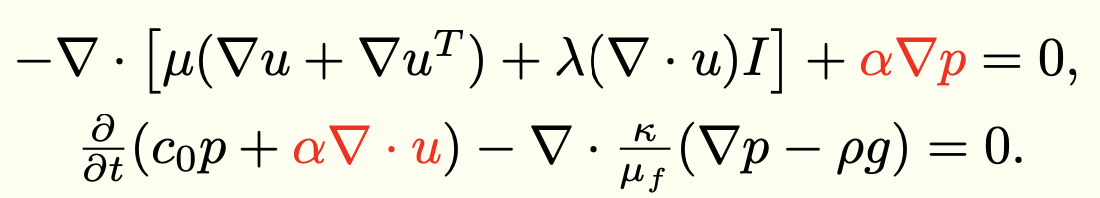
Example:
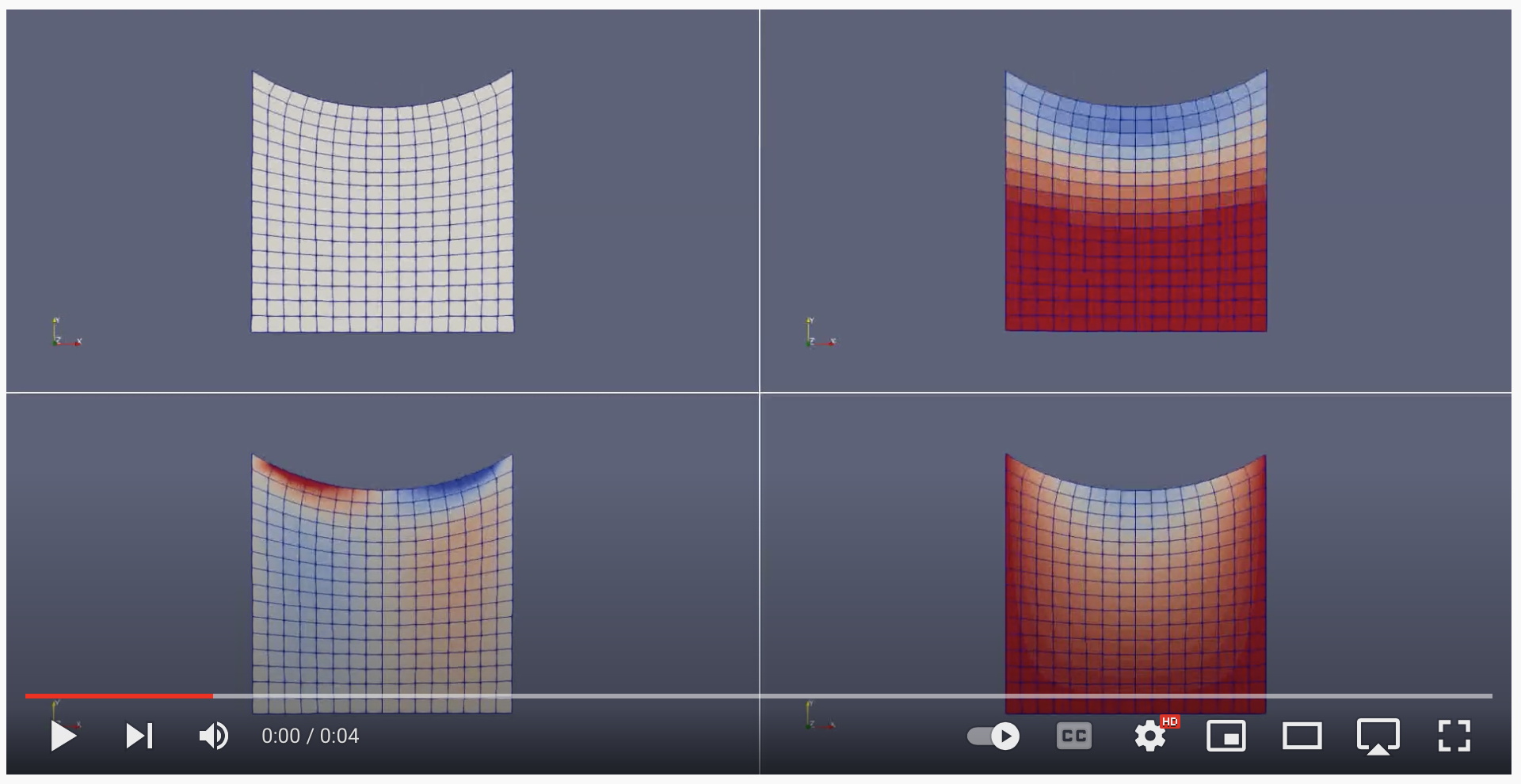
Terzaghi’s Problem; 1D soil compaction: Consider the compaction of a column of saturated soil with impermeable walls and bottom but with a free draining top (see figure on right for boundary conditions). When an external unit stress is applied on the top, the column of soil consolidates. The resulting pressure distribution can be solved for analytically using Biot’s equations. The simulation below shows the compaction of a column of soil using a sinusoidal force applied at the top of the of the column. Starting from the top left, the 4 sub-simulations show, in a clockwise order, the domain deformation, pore pressure, y-displacement and the x-displacement.
A 1D code in MATLAB to solve the Biot’s equations is written by the author here https://github.com/nvohra0016/Biot1D-MATLAB. The documentation has also been provided.
[Tp]: Energy with phase change: Stefan problem
The classical formulation of the Stefan problem allows one to solve for the domain and temperature of the different phases (eg. ice and water) [3]

By defining the enthalpy, the weak form can be derived.
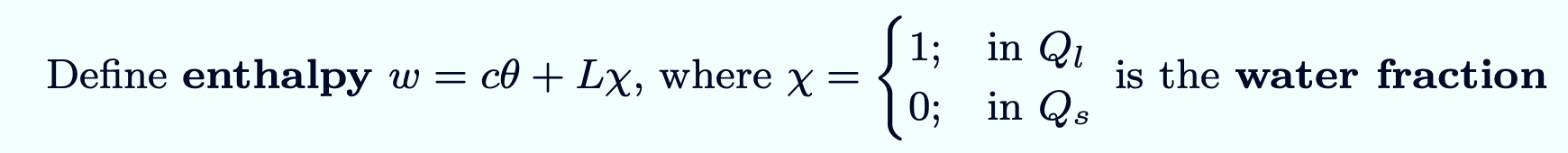
Application to Permafrost Modeling:
Permafrost is ground that remains frozen for two or more years. In the upper portion of permafrost, called the active layer, the temperature increases in the summer and decreases throughout the rest of the year. Hence the depth of this layer changes due to an increase of ambient temperature, and this causes the thawing of some portions of permafrost, which has further environmental consequences.
One of important features of permafrost is the presence of unfrozen water at low temperatures. This phenomenon is not fully explained, and is accompanied by lowering the freezing temperatures in small pores. A variety of algebraic expressions exist in literature to model the unfrozen water content. These are derived empirically. Consequently, the corresponding enthalpy curves are marked by an increased regularity that is absent in the Stefan problem [4], [5].

Example:
Estimating the extent of permafrost thaw: The simulation results the [Tp] model of permafrost thaw under warming climate conditions is shown below. The active layer depth can be estimated by tracking the 0 degree C isotherm. Assuming climate warming rate of 1 C/year, over 4 years, the model predicts that the depth of the active layer of a 5 meter column of permafrost increases by 4.5 times.

For a complete treatment of the equations and the numerical algorithm developed to solve the fully coupled [TpHM] system, the reader is refer to our work [6, 7].
References
[1] Biot, M. A. (1941), General theory of three-dimensional consolidation.
[2] Phillips, Wheeler (2007), A coupling of mixed and continuous Galerkin finite element methods for poroelasticity I: the continuous in time case.
[3] Visintin (1996), Models of Phase Transition.
[4] Osterkamp, Burn (2003), Permafrost.
[5] Nicolsky, Romanovsky, Tipenko (2007), Using in-situ temperature measurements to estimate saturated soil thermal properties by solving a sequence of optimization problems.
[6] Vohra, Peszynska (2024), Robust conservative scheme and nonlinear solver for phase transitions in heterogeneous permafrost.
[7] Vohra, Peszynska (2024), Iteratively coupled mixed finite element solver for thermo-hydro-mechanical modeling of permafrost thaw.